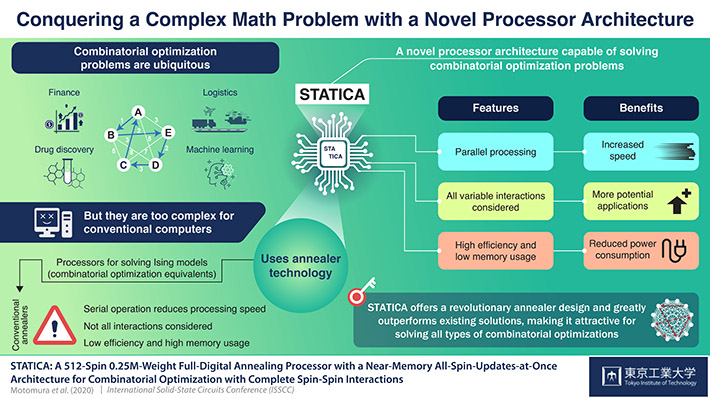
Scientists at Tokyo Institute of Technology have designed a novel processor architecture that can solve combinatorial optimization problems much faster than existing ones. Combinatorial optimization are complex problems that show up across many different fields of science and engineering and are difficult for conventional computers to handle, making specialized processor architectures very important.
The power of applied mathematics can be seen in the advancements of engineering and other sciences. However, often the mathematical problems used in these applications involve complex calculations that are beyond the capacities of modern computers in terms of time and resources. This is the case for combinatorial optimization problems.
Combinatorial optimization consists in locating an optimal object or solution in a finite set of possible ones. Such problems ubiquitously manifest in the real world across different fields. For example, combinatorial optimization problems show up in finance as portfolio optimization, in logistics as the well-known “travelling salesman problem”, in machine learning, and in drug discovery. However, current computers cannot cope with these problems when the number of variables is high.
Fortunately, a team of researchers from Tokyo Institute of Technology, in collaboration with Hitachi Hokkaido University Laboratory, and the University of Tokyo, have designed a novel processor architecture to specifically solve combinatorial optimization problems expressed in the form of an Ising model. The Ising model was originally used to describe the magnetic states of atoms (spins) in magnetic materials. However, this model can be used as an abstraction to solve combinatorial optimization problems because the evolution of the spins, which tends to reach the so-called lowest-energy state, mirrors how an optimization algorithm searches for the best solution. In fact, the state of the spins in the lowest-energy state can be directly mapped to the solution of a combinatorial optimization problem.
The proposed processor architecture, called STATICA, is fundamentally different from existing processors that calculate Ising models, called annealers. One limitation of most reported annealers is that they only consider spin interactions between neighboring particles. This allows for faster calculation, but limits their possible applications. In contrast, STATICA is fully connected and all spin-to-spin interactions are considered. While STATICA’s processing speed is lower than those of similar annealers, its calculation scheme is better: it uses parallel updating.
In most annealers, the evolution of spins (updating) is calculated iteratively. This process is inherently serial, meaning that spin switchings are calculated one by one because the switching of one spin affects all the rest in the same iteration. In STATICA, the updating process is carried out in parallel using what is known as stochastic cell automata. Instead of calculating spin states using the spins themselves, STATICA creates replicas of the spins and spin-to-replica interactions are used, allowing for parallel calculation. This saves a tremendous amount of time due to the reduced number of steps needed. “We have proven that conventional approaches and STATICA derive the same solution under certain conditions, but STATICA does so in N times fewer steps, where N is the number of spins in the model,” remarks Prof. Masato Motomura, who led this project. Furthermore, the research team implemented an approach called delta-driven spin updating. Because only spins that changed in the previous iteration are important when calculating the following one, a selector circuit is used to only involve spins that flipped in each iteration.
STATICA offers reduced power consumption, higher processing speed, and better accuracy than other annealers. “STATICA aims at revolutionizing annealing processors by solving optimization problems based on the mathematical model of stochastic cell automata. Our initial evaluations have provided strong results,” concludes Prof. Motomura. Further refinements will make STATICA an attractive choice for combinatorial optimization.